Les lunules d'Hippocrate
Vers 430 avant J.C., Hippocrate de Chio, mathématicien grec, a démontré que :
la somme des aires des quatre lunules est égale à l'aire du carré ABCD.
La démonstration est du niveau 4e. |
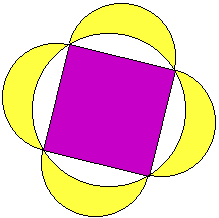 |
Les lunules d'HippocrateVers 430 avant J.C., Hippocrate de Chio, mathématicien grec, a démontré que :
|